Research Overview
Nonnegativity and Polynomial Optimization
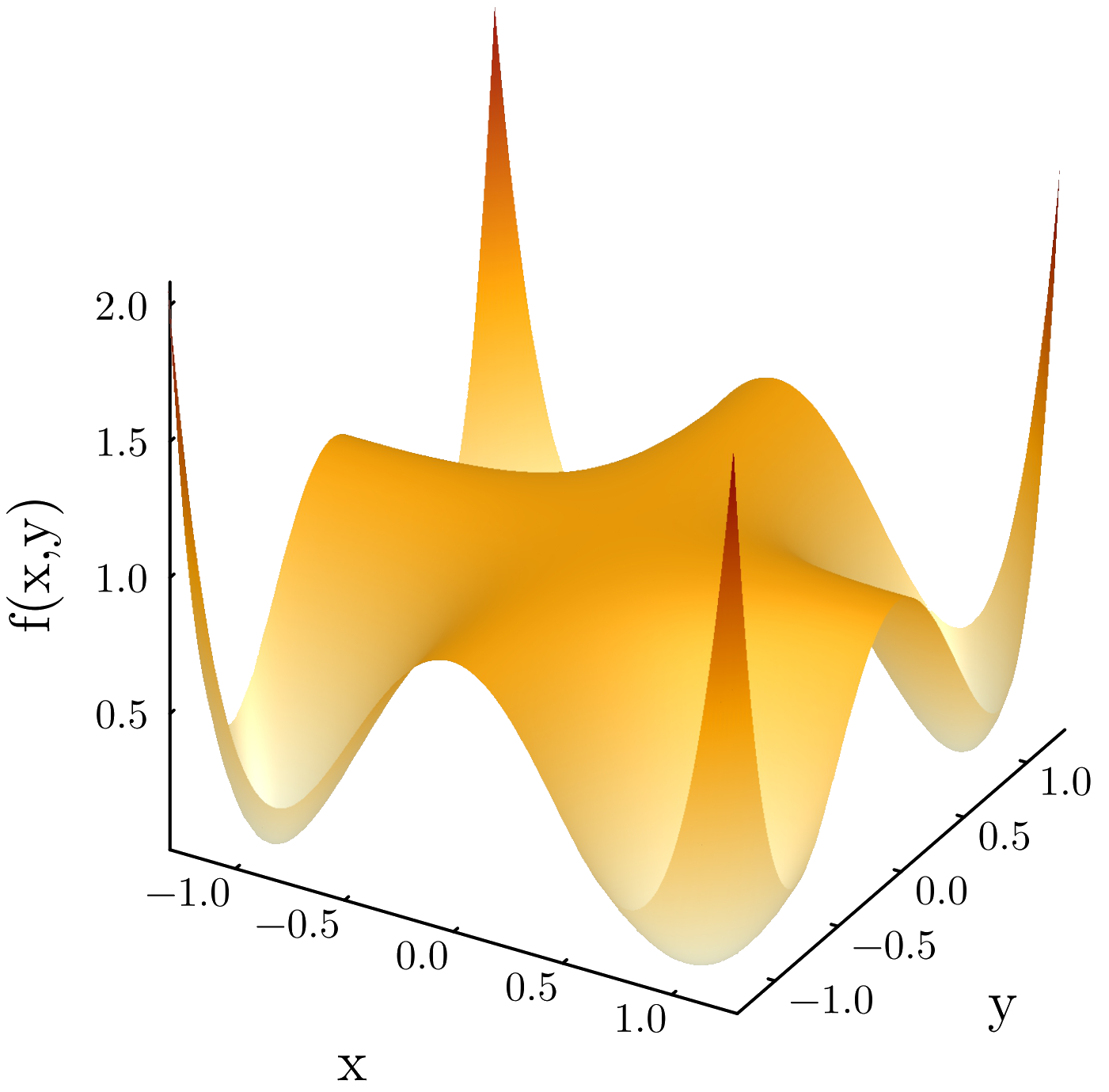
A (constrained) polynomial optimization problem (CPOP) consists of minimizing a multivariate real polynomial $f \in \mathbb{R}[\mathbf{x}] = \mathbb{R}[x_1,\ldots,x_n]$ over a basic semi-algebraic set, which is defined by finitely many polynomial inequalities. These types of problems are in general non-convex, and notoriously hard to solve. E.g., even CPOPs of total degree at most four already contain NP-complete problems. At the same time CPOPs are a very broad class, containing problems from applications in dynamics, logistics, computer vision, theoretical computer science, finance, quantum physics, data science, and more. Minimizing a polynomial is essentially equivalent to certifying nonnegativity of real polynomials $f(\mathbf{x})$ in $\mathbb{R}[\mathbf{x}]$, i.e., $f(\mathbf{x}) \geq 0$, for all $\mathbf{x}$ in $\mathbb{R}[\mathbf{x}]$. This a classical question from real algebraic geometry dating back in the 19th century. Famously, David Hilbert proved in 1888 that there exists nonnegative polynomials that cannot be written as a sum of squares, which let to Hilbert's 17th problem. The first published example of such a polynomial was given by Motzkin in 1967, see figure. During the last 25 years, the mathematical theory around polynomial optimization problems progressed substantially, after fundamental contributions by Lasserre and Parillo in the early 2000's. Due to the dificulty to certify nonnegativity, one uses certificates of nonnegativity. These are, roughly speaking, conditions that 1. imply nonnegativity, 2. are easier to test than nonnegativity and 3. are satisfied for a significant amount of polynomials.
Sums of Nonnegative Circuit Polynomials
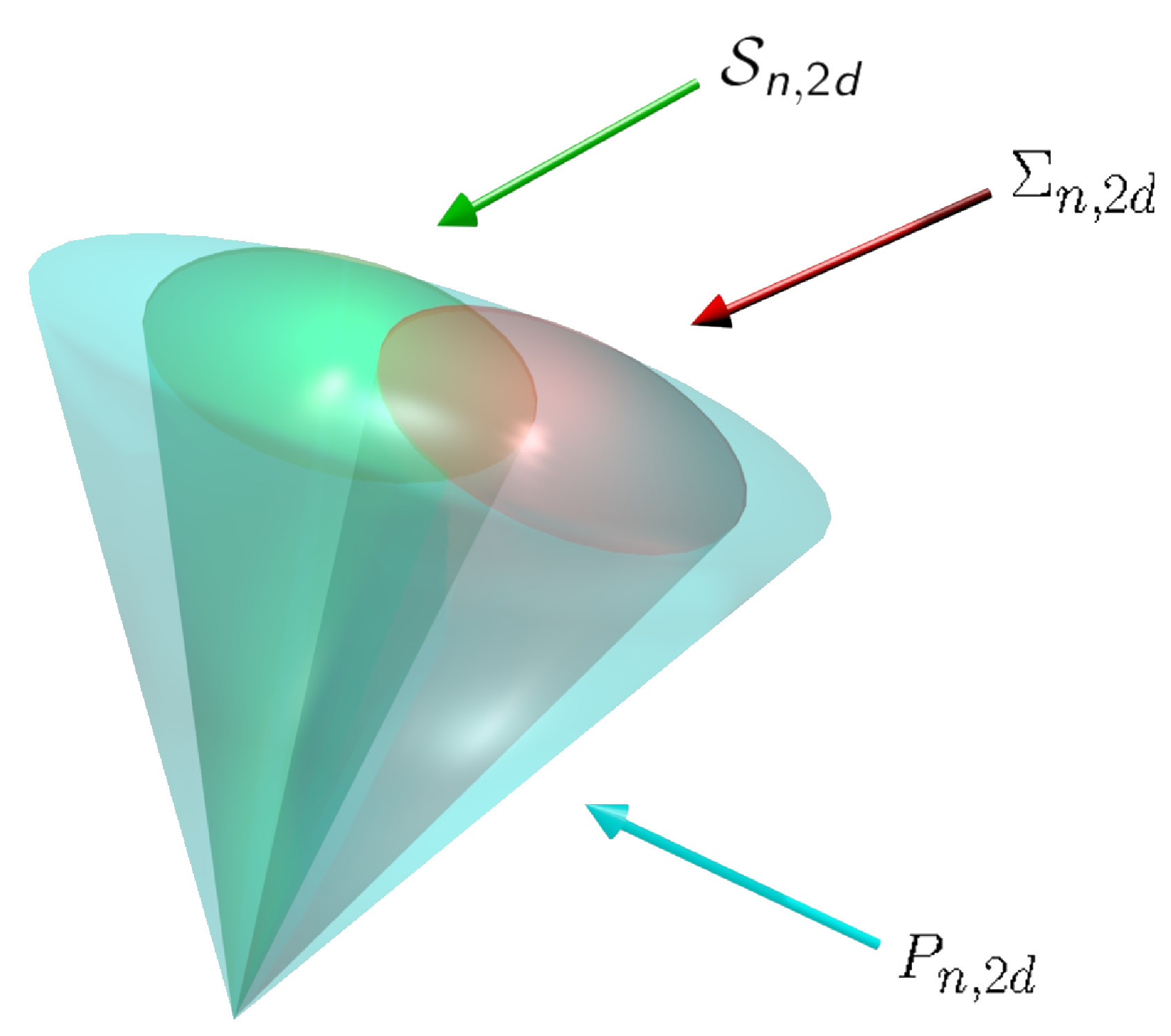
In 2014, Iliman and de Wolff suggested a new certificate of nonnegativity called sums of sums of nonnegative circuit polynomials (SONC). The fundamental observation for this certificate is that for polynomials, which are supported on a circuit, i.e., a minimally affine dependent support set, it is extremely easy to certify nonnegativity. Furthermore, this certificate forms a full-dimensional convex cone, which intersects the SOS cone, but is not contained in it. SONCs are a natural generalization of AGIforms, which were pioneered by Reznick already in 1989. Also, independently Chandrasekaran and Shah developed briefly afterwards a certificate called SAGE for signomial programming. Nowadays, thanks to Wang, we know that "SONC = SAGE", and a SONC (SAGE) decomposition can, in sharp contrast to SOS, always be achieved on the support of the initial polynomial, which is supposed to be certified. Moreover, SONCs can effectively be detected a relative entropy programming, a convex optimization problem, and admit construction of converging hierarchies of nonnegativity. The picture shows schematically the cones of nonnegative polynomials, sums of squares, and SONCs.
Applications of Nonnegative Circuit Polynomials
Sums of nonnegative circuit polynomials are not merely a theoretical concept of nonnegativity, but over the past years we applied them for tackling various applications in science and engineering.
One area of application are chemical reaction networks (CRN).
These model the dynamic behavior of biochemical processes via underlying parametrized ODEs.
Here, we applied SONCs to identify parameter regions of reaction rates leading to mono- vs. multistationarity for phosphorylation networks, which play an important role e.g., in cell signaling.
 Another area of application are dynamical systems.
Here, a central goal is certifying stability, which one can achieve via construction of Lyapunov functions.
It turns out that, similar as SOS, SONCs can be used for searching such functions, leading to interesting combinatorial problems on support sets of polynomials.
Another area of application are dynamical systems.
Here, a central goal is certifying stability, which one can achieve via construction of Lyapunov functions.
It turns out that, similar as SOS, SONCs can be used for searching such functions, leading to interesting combinatorial problems on support sets of polynomials.
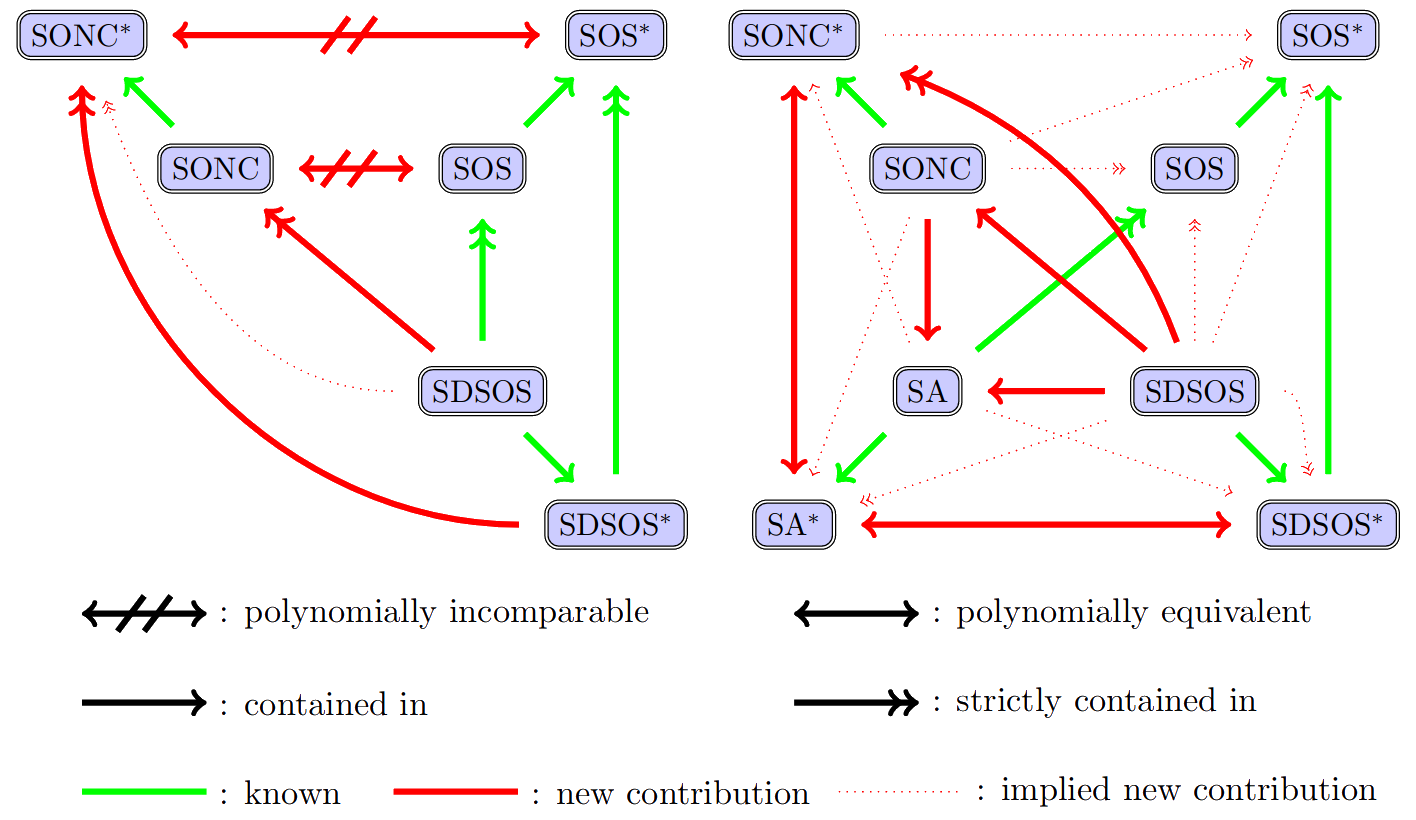
A third area of application is theoretical computer science.
SONCs are a meaningful certificate in terms of proof systems analyzing the complexity of central NP-complete algorithms like MAXCUT.
mathematically, these proof systems are polynomial optimization problems on the Boolean hypercube (BCPOP).
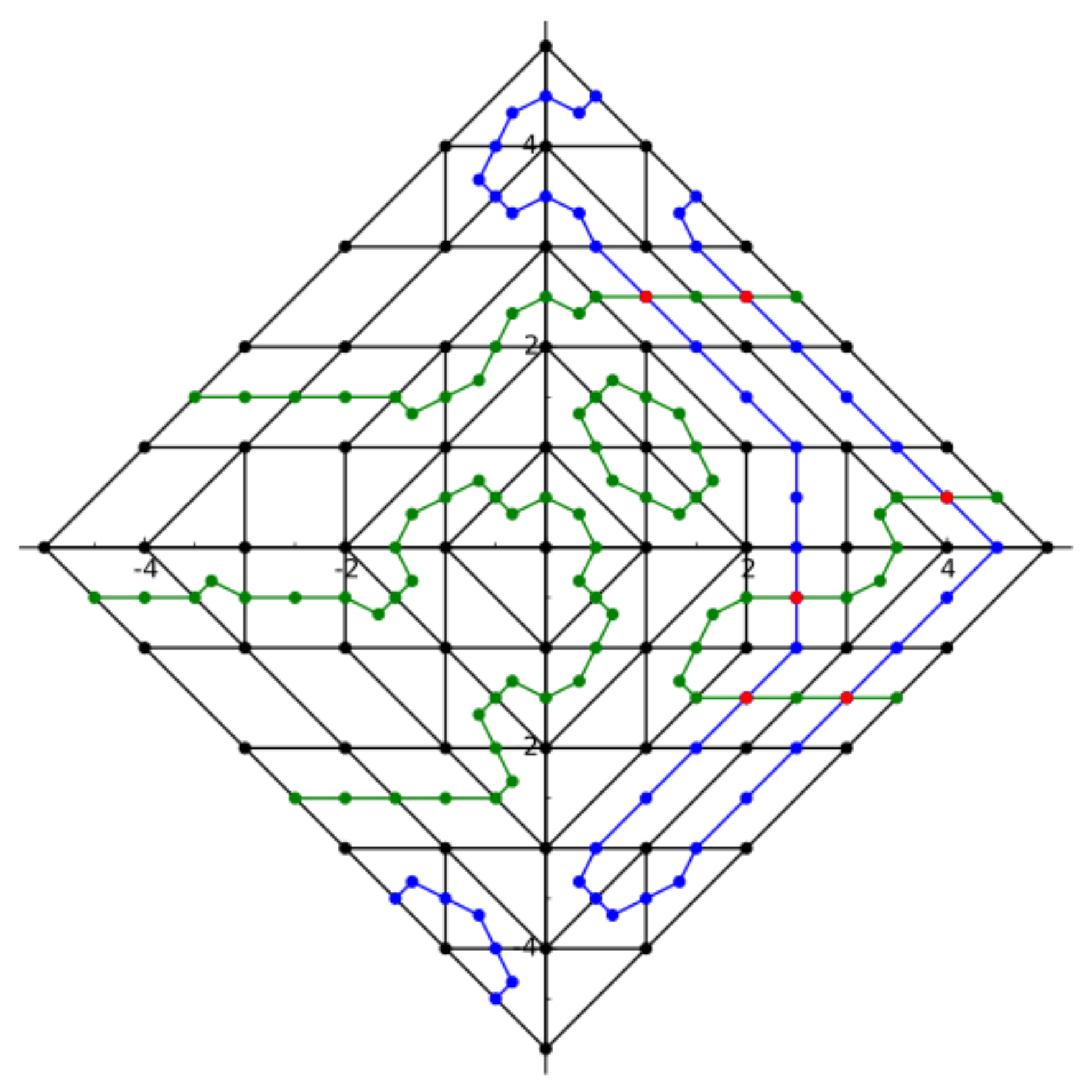
We showed, among other results, that, as expected due to reasons related to the Unique Games Conjecture, SONCs are not polynomially equivalent to SOS on BCPOPs; see right figure.
Algorithmic and Applied Algebra
Algebraic structures are covering a major part of the mathematical universe.
They are, moreover, omnipresent in various subjects in the natural sciences and engineering, and hence in various applied problems.
Often, however, these algebraic structures are not obvious at the first glance.
Applied algebra uncovers algebraic structures, and exploits them in order to achieve an improved understanding of the applied subject and / or to tackle the problem at hand more effectively.
The latter requires algorithmic and often also data based approaches.
Main problems in this area are (next to polynomial optimization) effective solving of systems of polynomial equations.
This can be achieved symbolically involving Gröbner bases or numerically using homotopy continuation.
In this context, often the real or real positive solutions of the system are of particular interest.
This provides additional computational challenges and often requires investigation of abstract algebraic entities as discriminantal structures.
Other areas of application may involve topological properties such as homotopy of homology, which admit algebraic questions.
Moreover, many applied problems can be tackled with methods of computational discrete geometry such as polyhedral complexes, which often have rich and fascinating interplays with algebraic structures.
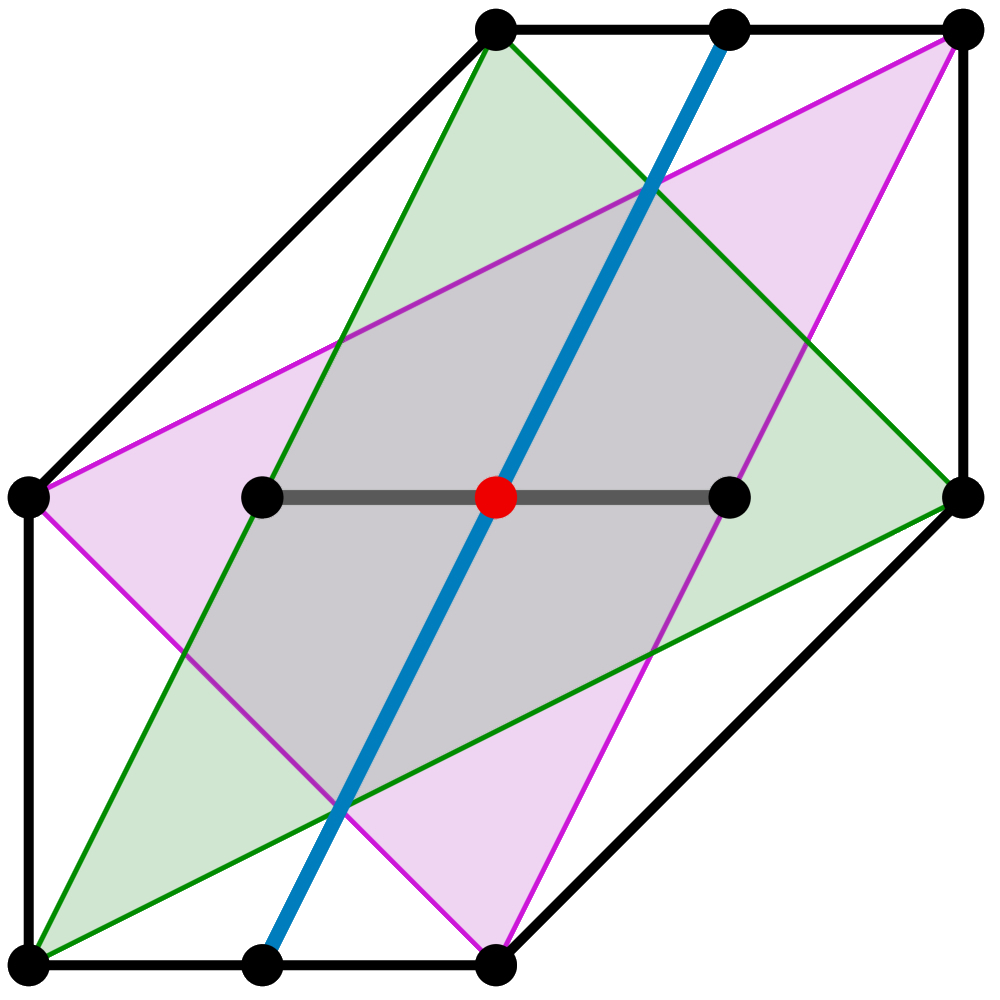
Our group pursues various reserach interests in the broader realm of algorithmic and applied algebra.
The picture on the left shows one example: an implementation of Viro's patchworking -- a combinatorial algorithmic methods that yields information on real loci of hypersurfaces and real solutions of polynomial systems.
Further Areas of Optimization and Relations to Quantum Computing
Starting in the 1930s with routing, scheduling and network design problems combinatorial optimization rose to a large research field, that is closely related to industry and driven by computational efficiency.
With the invention of NP-completeness, one could distinguish the computational hardness of problems and approach solving them differently.
For many NP-complete problems like the Traveling Salesmen Problem not only exact algorithms, but also heuristics were developed.
Our group works on algorithm design, experimental comparison, and application of such algorithms and heuristics.
For example, one of these is the Lin-Kernighan-Helsgaun heuristic, that takes a route as an input and locally optimizes this tour by deleting and adding edges iteratively.
We developed a new variant of this heuristic, that is experimentally 13% faster on average on large instances with more than 30000 nodes.
 While at first each combinatorial optimization problem was tackled individually, the invention of linear programming enabled tackling all of them with the same approach: graph based problems like TSP or maximum-flow problems could be described in the same way as scheduling problems.
For linear (non-integer) problems the Simplex algorithm was a big milestone, that lead to solving even large optimization problems in seconds.
Based on the Simplex algorithm several methods like Branch-and-Bound for integer methods were developed depending on the performance of the Simplex algorithm.
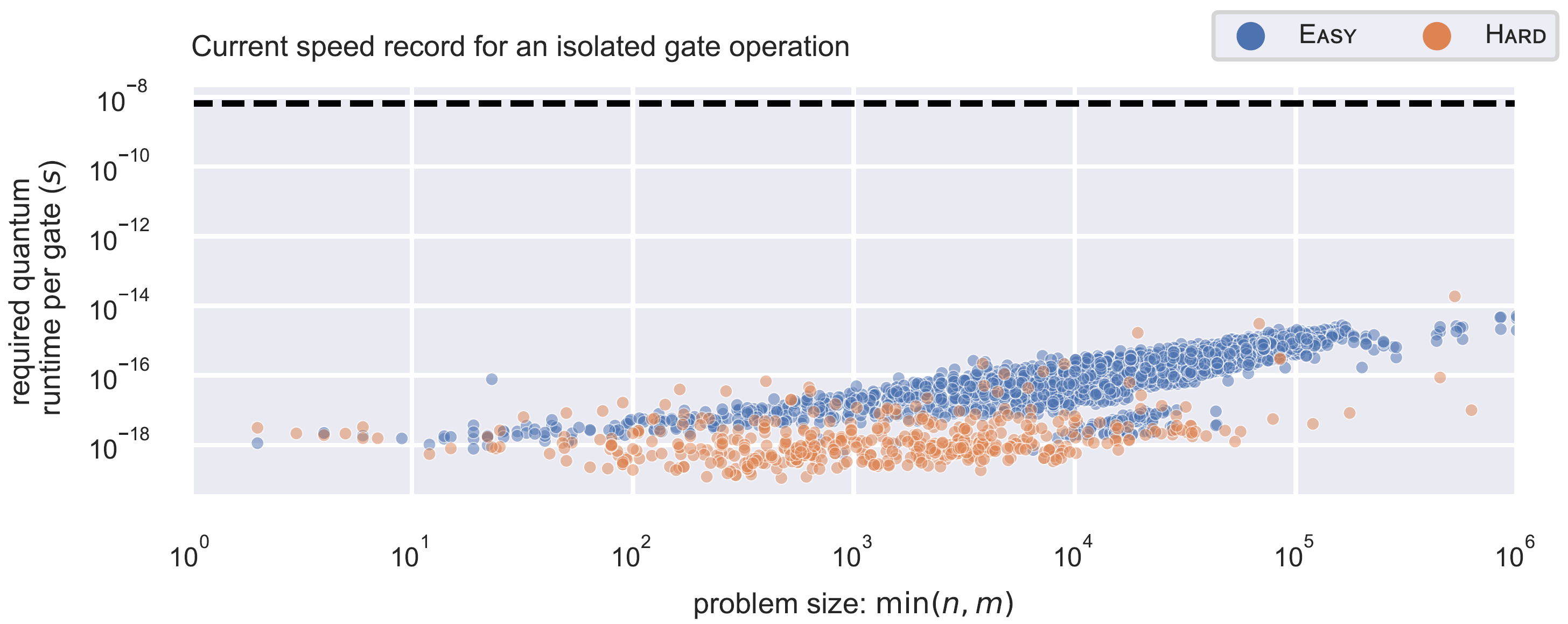
Recently, quantum computing had a large impact on combinatorial optimization trying to solve these problems with quantum algorithms or hybrid methods.
For example, Nannicini proposed a quantum version of the simplex method, stating a clear asymptotic advantage over the classical version.
As part of the ProvideQ project we performed a realistic runtime analysis, comparing the number of gates needed for the computation with the runtime needed by the classical version.
While at first each combinatorial optimization problem was tackled individually, the invention of linear programming enabled tackling all of them with the same approach: graph based problems like TSP or maximum-flow problems could be described in the same way as scheduling problems.
For linear (non-integer) problems the Simplex algorithm was a big milestone, that lead to solving even large optimization problems in seconds.
Based on the Simplex algorithm several methods like Branch-and-Bound for integer methods were developed depending on the performance of the Simplex algorithm.
Recently, quantum computing had a large impact on combinatorial optimization trying to solve these problems with quantum algorithms or hybrid methods.
For example, Nannicini proposed a quantum version of the simplex method, stating a clear asymptotic advantage over the classical version.
As part of the ProvideQ project we performed a realistic runtime analysis, comparing the number of gates needed for the computation with the runtime needed by the classical version.
Machine Learning
Machine learning is a field that exploded in recent years - in particular due to the rapid development of neural networks and their easy usability via software ly PyTorch and TensorFlow.
The fields of application and opportunities arising from their usage are countless.
In our applied algebra group we use neural networks in various interdisciplinary research project joint with partners, who provide problems and data.
We work on the implementation, data understanding, modeling, and further related mathematical questions.
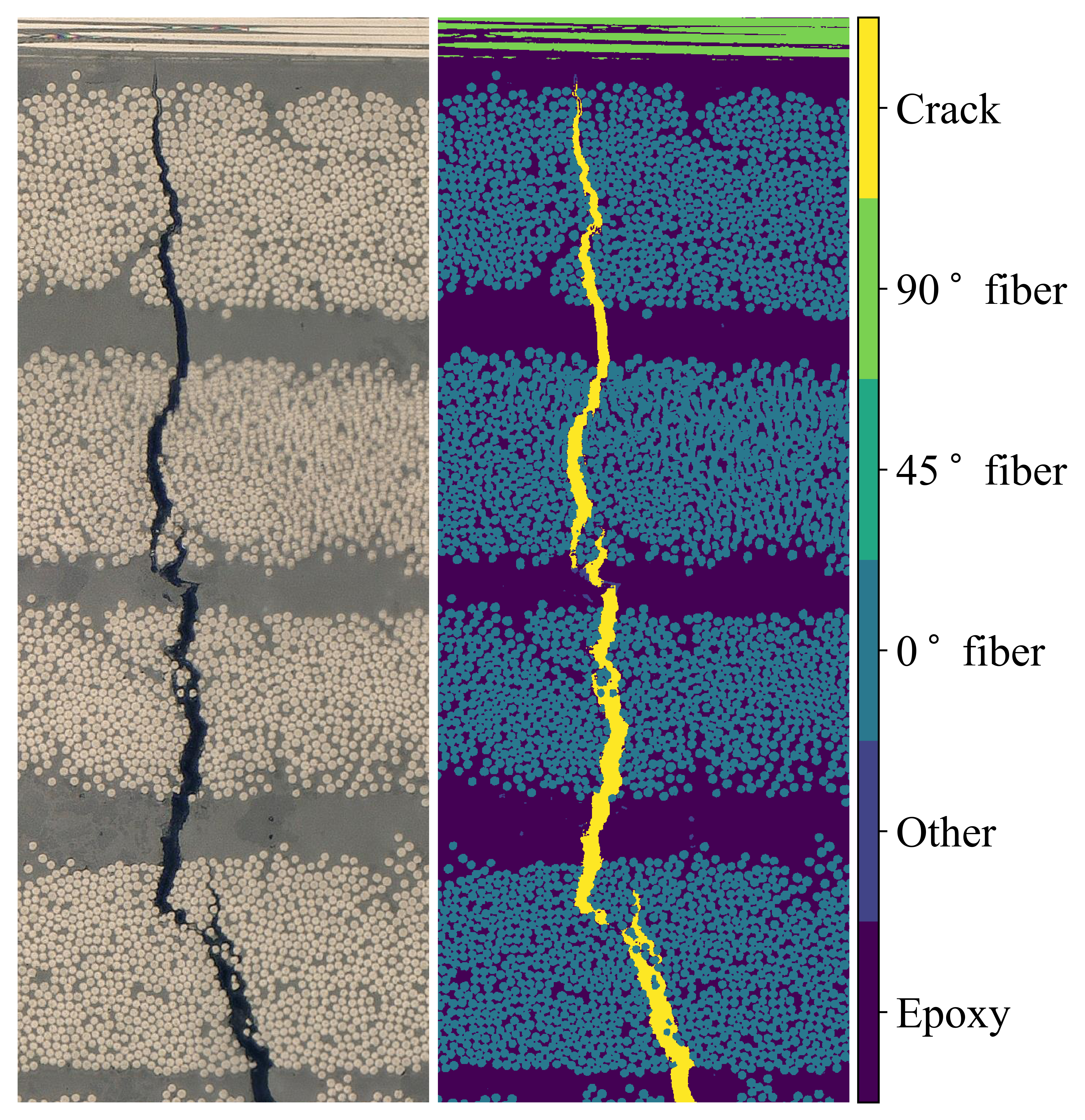
Currently, we are particularly active in the analysis of image data, which machine learning can greatly automate and accelerate.
For example, in the field of composite material research, the very same is generated very frequently,
for instance in the form of micrographs to investigate material characteristics on the micro-level.
Current and potential tasks include object detection or image classification for quality assurance of the manufacturing process,
semantic segmentation allowing for detailed subsequent analyses on the fiber level and crack detection (see picture on the right).
Geometric Materials
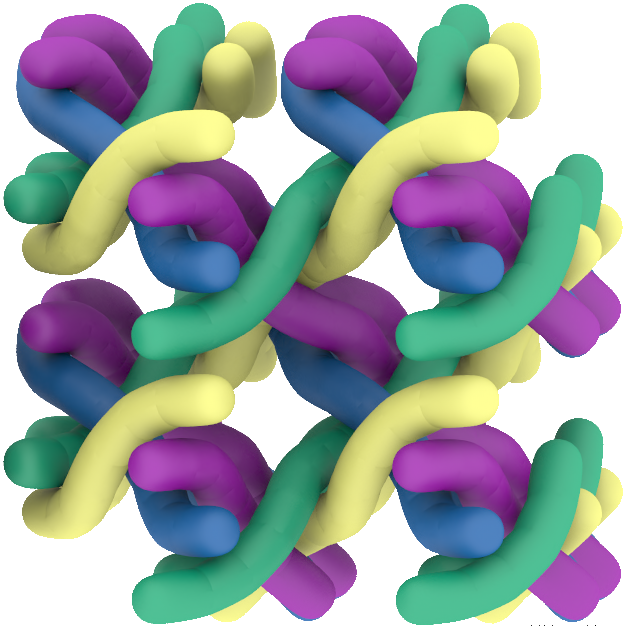
Ranging from micro- to macroscale and from animate to inanimate structures, principles of geometry appear in numerous materials. Geometric concepts can be observed in animate in inanimate objects such as plant physiology, self-assemblies, crystallization and foam; associated principles are used in the design of metamaterials with prescribed microstructures and targeted functionality. In many of these scenarios, the geometry emerges through the minimization of energy functionals in combination with geometric constraints that are typically given as polynomial (in-)equalities. This highlights a clear connection between (algebraic) geometry, mathematical optimization and the geometry of materials that is investigated in this area. The picture on the left shows the $\Sigma^+$ cylinder packing, which exhibits an auxetic expansion under strain, meaning that it exhibit a perpendicular expansion upon stretching the material in a chosen direction; a somewhat counterintuitive material property.